
実験基礎論 (学部2年生 前期 水曜日2限,合成実験室) 更新日 2021.2.19
実験基礎論②実験結果が出たら
安全、正確、迅速な実験を行うためには、基本操作をしっかりと身に付けることが不可欠である。ここでは、応用化学実験を実施するために必要な基本操作(応化実験Ⅰ、テキスト「基本操作」)を解説する。また、応化実験内では使わない一般的な基本についても紹介する。
| 1 実験の基本操作 |
| 2 データ解析 |
| 2.1 有効数字 |
| 2.2 誤差 |
| 2.3 統計学 |
| 2.4 グラフ |
| 2.5 表 |
| 2.6 参考文献 |
| 3 成果のまとめ方 |
データ解析
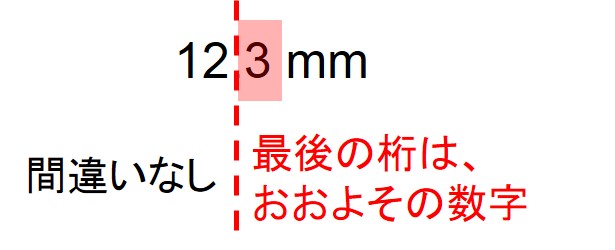
| 目盛を読み取るときには目盛間まで読み取って有効数字とする。例えば\(\rm 1 mm\) 刻みの定規で長さを測るときには、\(\rm 0.1 mm\) まで読み取る。当然最後の桁は個人差が生じるし、同じ測定者でも計り直すと少々ずれるかもしれない。つまり、有効数字の最終桁は個人差の表れる数字である。\(\rm 12.3 mm\) と読み取った場合、真の値は\(\rm 12.4 mm\) かもしれないし、\(\rm 12.2\) 、あるいは\(\rm 12.1 mm\) かもしれないという意味を含んでいる。読み取り誤差の他に、計器自体の誤差もあるので、誤差の評価には注意する。 |
 |
| 誤差の伝播 ある値を求めるときに、複数の測定値から求めることが多い。このとき、有効数字の扱いが問題になる。有効桁数の異なる値を足したり引いたり掛けたり割ったりするわけであるが、ここに三角関数や対数などが入ってくると、求めた値の有効数字が一体いくつになるのか分からなくなる。このような場合の評価の仕方については、例えば参考文献[1]などに厳密に議論されているので、ここでは直感的に分かり易く考えることにする。 原点に立ち戻って考えると、誤差なく求まる桁プラス一桁が有効数字であるので、求める値が大きくなるように、あるいは小さくなるように元の数字を全てわざとずらしてみると良い。例えば立方体の一辺の長さが\(\rm 12.3 mm\) であったとき、\(\rm 12.3\) の\(\rm 3\) 乗と\(\rm 12.4\) の\(\rm 3\) 乗を比べ、どの桁から異なっているか調べて有効数字を決めると良い。 同様にして誤差の大きい(有効桁数の少ない)測定値と少ない測定値からある値を求めた場合、誤差の大きい値に支配される。例えば3桁の値と4桁の値を四則演算した場合には、有効数字は3桁となる。三角関数や対数など、計算が複雑になる際には注意して吟味する必要がある。 有効数字の表記 数字の表記は、有効数字を明らかにするために、\(\rm 12.3 mm\) とするより、\(\rm 1.23 \times\ 10^{-1} \ mm\) とすることが望ましい。 |
 |
| データの意味合いは、誤差の大きさに強く依存している。例えば今日のおやつの時間は3時と言われたときに、実は誤差2時間だったとすると、お昼ご飯か夕ご飯に差し掛かってしまう。おやつの時間が2時50分であったり、3時15分であったり、3時を中心に前後10分から15分程度に収まっている、というような情報は不可欠である。有効数字は1回のデータの測定分解能を示すものであることから、次に測定したときにどのような値を与えるかについては何ら物語っていない。まず、誤差に2種類あることから理解する必要がある。 精度と確度
系統誤差と偶然誤差についても説明しておこう。
① 測定を十分な回数行って平均値を求める ② ばらつきを評価し、誤差を見積もる ことだけである。①、②両立して初めて活用できるデータとなることを意識する必要がある。 S/N比 誤差ではないが、S/N比についてもここで紹介しておこう。Sはシグナル(Signal)、Nはノイズ(Noise)を表す。測定機器における電気的、磁気的なノイズがスペクトルなどに現れることがしばしばあり、精密測定においては避けられない。ノイズが大きい場合にはシグナルが隠れたり、シグナルとノイズの判別がつかなかったりすることがある。しかしながらほぼある一定の強度で現れるシグナルに対し、ノイズはランダムに出現する。このため、繰り返し測定して積算すると、シグナルとノイズを判別できるようになる。このときのシグナルとノイズの強度比をS/N比と呼ぶ。 測定回数をnとしたとき、S/N比は\( \sqrt{n} \)に比例する。S/N比を2倍にしたければ積算回数を4倍に、S/N比を3倍にしたければ積算回数を9倍にすればよい。 |
| まず、用語の説明をする。科学的な測定についての観点で解釈した場合の説明であり、一般的な統計学とは多少のずれがあるので注意してもらいたい。 [標本(sample)、母集団(parent population)、抽出(sampling)] 母集団が大き過ぎる場合、その構成要素すべてを吟味できない。そこで母集団から無作為に標本を抽出し、母集団の統計量を推測する。 測定では精度、確度の問題から、真の値が得られることはない。精度の十分に高い測定では、繰り返し測定すると真の値近辺でばらついた測定値が得られる。このとき、“母集団”は無限回測定したときに各測定で得られる値すべてであり、有限回測定したとすると、その測定値はその中から“標本”を“抽出”したことになる。 [平均値(mean)、中央値(median)、最頻値(mode)] 母集団の特性を代表値で表す際に、標本の平均値、中央値、あるいは最頻値を用いる。身体測定や収入調査などの統計処理については大きくずれた1点が多大に影響する場合など平均値が不適当なこともあるが、科学的な測定のほとんどは平均値で議論する。これは確度の低下がばらつきに由来し、多くの場合にそのばらつきが正規分布を示すと仮定できるからである。正規分布については後述する。 ある測定を\(\it n \) 回繰り返したときの測定値をそれぞれ\(x_1, x_2,\cdots,x_n \)とすると、平均値(標本平均値)\(\overline{x} \)は、\[\overline{x} = \frac{\it x_\rm1 +\it x_\rm2 + \cdots + \it x_\rm n}{n}=\frac{1}{n}\sum_{i=1}^{n}x_i \]と書ける。これに対し、母集団の平均値(母平均)は\(\mu\)で表される。系統誤差が無い場合には、\(\mu\) は測定で求めたい真の値と一致する。 [分散(variance)、標準偏差(standard deviation)] 集団の特性をより正確に表現するためには、平均値に加えて値のばらつきを示す必要がある。平均値を中心に測定値が分布しているため、その差\((x_i-\overline{x})\) を評価すればよい。\((x_i-\overline{x})\) には正の場合と負の場合があることから、2乗平均を取って\[s^2=\frac{1}{n}\sum_{i=1}^{n}(x_i-\overline{x})^2\]とする。このときの\(s^2\)を標本分散、\(s\)を標本標準偏差と呼ぶ。一方、母分散と母標準偏差はそれぞれ\(\sigma, \sigma^2\)で表される。 ただし、この評価方法では常に\(s^2<\sigma^2\)となって母標準偏差よりも大きく見積もってしまうため、\(n\) の代わりに\(n-1\) を用いて、\[u=\sqrt{\frac{1}{n-1}\sum_{i=1}^{n}(x_i-\overline{x})^2}\] とした方が、\(u\) は\(\sigma\) のよい近似となる。このときの\(u^2\) は不偏分散と言う。通常、標準偏差と呼ぶものは\(u\) のことであり、標本標準偏差とは区別する。 [正規分布 (ガウス分布)] 「\(n\) 回コインを投げて表が出た回数を数える」という作業を何度も繰り返し、表が出た回数を横軸に、その頻度を縦軸に取ったグラフを作ると、作業回数が増えるにしたがって鐘形曲線が現れる。これを二項分布と呼ぶ。これに対し、「サイコロを\(n\) 回振った合計を求める」という作業を繰り返して、同様のグラフに示すとやはり似たような鐘形曲線が現れる。このような分布を正規分布と呼ぶ。他にも多数の分布関数(熱力学において平衡状態の気体分子の速度を記述するマクスウェル=ボルツマン分布など)があるが、通常は正規分布を仮定して解析を行う。 測定値はどの程度正しいか? 次の2点を仮定して考える。 ① 系統誤差を持たない、② 偶然誤差は平均値\(\mu\)、標準偏差\(\sigma\)の正規分布に従う 得られた測定値が真の値に対してどの程度ずれがあるか評価してみよう。\(\sigma\)が小さければ測定値はほぼ\(\mu\)の近辺、大きければずれた値を示している確率が高い。この確率は正確に見積もられ、\(\mu\pm\sigma\) の範囲に測定値が得られる確率は68.27 %である。\(2\sigma,3\sigma\) も含めてまとめると、\[\mu\hspace{1mm}\pm\sigma:\hspace{3mm}68.27\hspace{1mm}\%\] \[\mu\pm2\sigma:\hspace{3mm}95.45\hspace{1mm}\%\] \[\mu\pm3\sigma:\hspace{3mm}99.73\hspace{1mm}\%\]となる。真の値\(\mu\) を横軸の原点にして図示すると、正規分布にしたがう限り、下図のように\(\sigma\) に対して常に確率分布が一定となる。 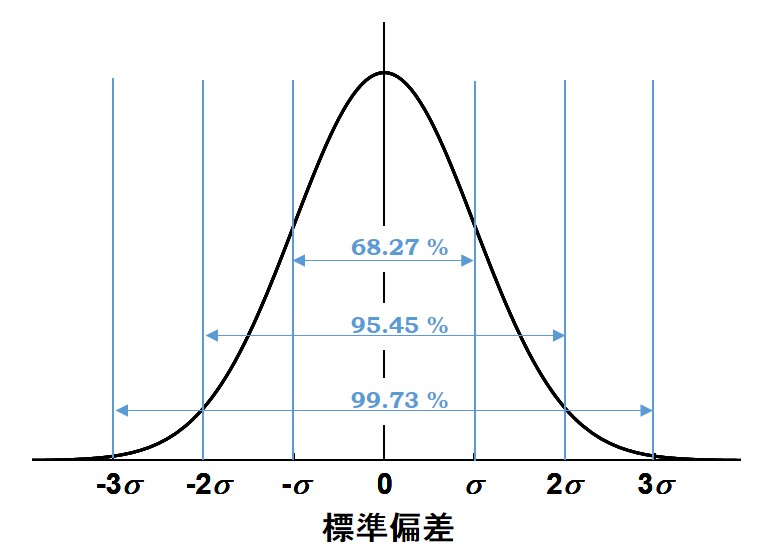 逆に測定を\(n\) 回行って平均値\(\overline{x}\)と標準偏差\(u\)を得た場合、真の値\(\mu\) がどの程度\(\overline{x}\) から離れているか、その確率分布は自由度\(n-1\) に依存したものとなり、Studentのt分布と呼ばれる。グラフ作成時にエラーバー(信頼限界)を付ける際に用いられる概念である。詳細は参考文献[1]などの専門書にお任せするとして、信頼度\(z \%\) のエラーバーはt分布におけるt値を用いて、\[\overline{x}\pm \frac{tu}{\sqrt{n}}\] と書ける。t値は計算もできるが、t分布表から読み取ると便利である。測定回数を増やすとエラーバーは減少するが、減少の仕方は信頼度に依って異なる。下図の測定回数\(n\)に対する\(\frac{t}{\sqrt{n}}\) の依存性を参照し、適当な\(n\)を設定して測定するとよい。 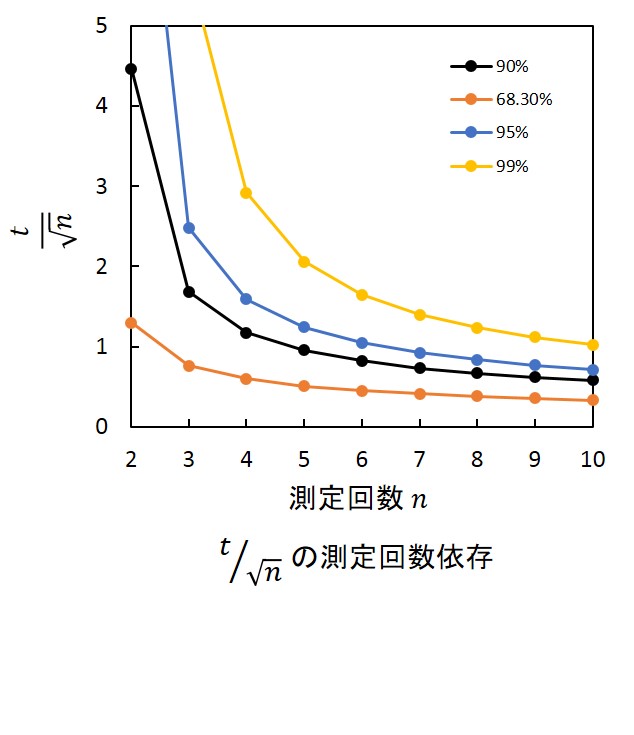 |
|
形式 軸、目盛、軸表示、単位を適切に示す。またデータが複数の場合には、マーカーや線の種類や色で見易いように区別し、必要に応じて凡例を示す。レポートや論文の場合には、グラフは図に分類され、通し番号をつける。表は図とは別系統の通し番号をつける。グラフの下に、タイトルとともにキャプションをつけ、キャプションを読んで大まかな内容が理解できるようにする。下に例を載せておく。 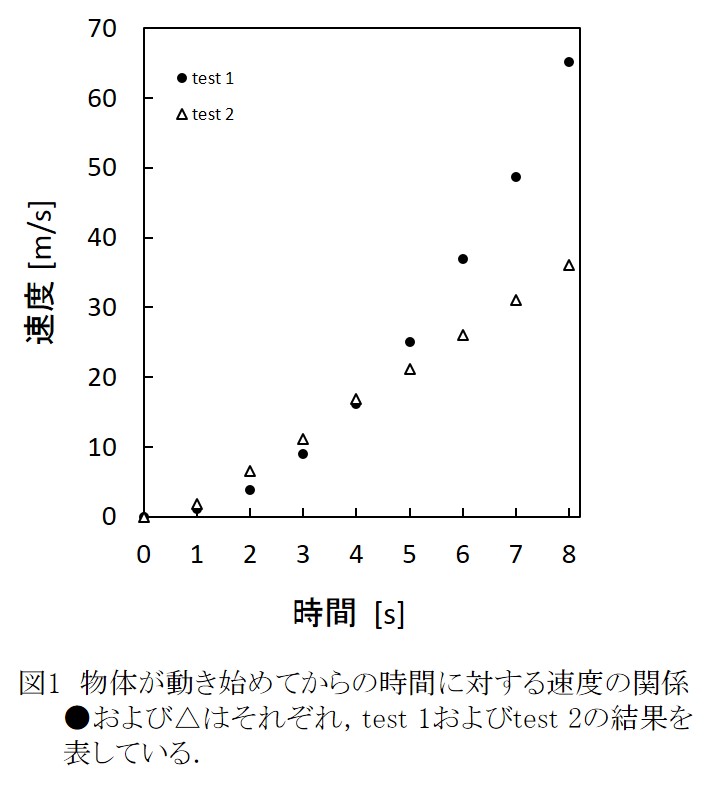 エラーバー (信頼限界) グラフに測定点を示すときには、必ずエラーバーを付けるのが原則である。エラーバーがない場合は、測定点内に収まるほど確度が高い、即ち偶然誤差の小さな測定であったことを意味する。 エラーバーは上述(2.3節)したように、Studentのt分布を利用して評価できる。測定点の上下にエラーバーを描き、その範囲を示す。 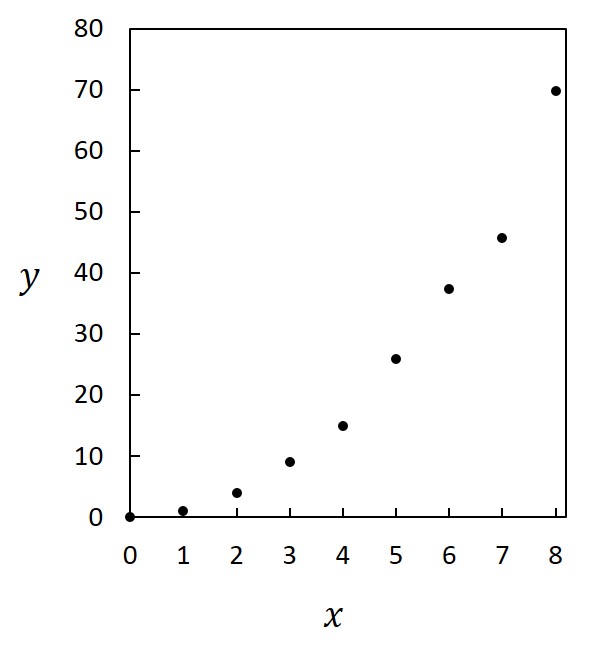 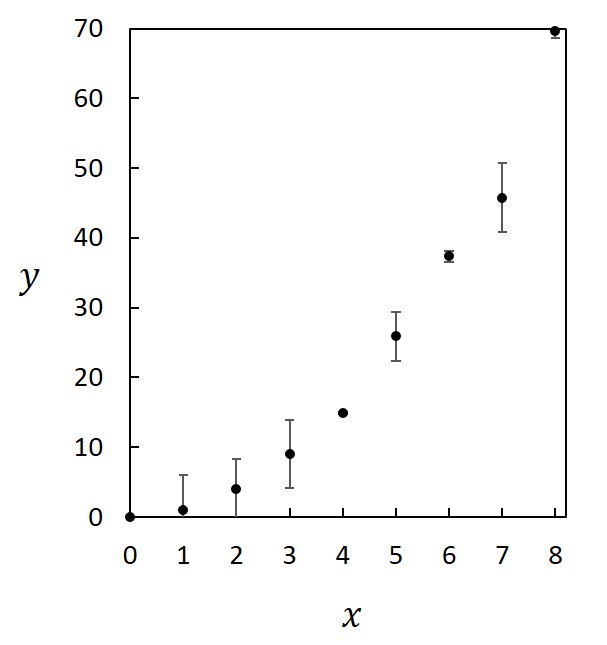 測定点のつなぎ方 測定点のつなぎ方には以下のような方法がある。
1. 直線 ごく一部の例外を除き、直線がデータ間の振る舞いを表現していることは期待できない。人為的要素は少ないとは言え、誤った印象を与える可能性は強く、直線でつなぐならむしろデータ間をつながない方が得策であろう。 ただし、横軸に取る変数が離散的(とびとび)であり、その変数に対して連続的にデータがある場合には直線でつなぐのが適切である。例えば原子番号に対する何らかの挙動などを示すような場合である。また、直線に見えなくなるくらいにデータが密な場合にはデータ点を示すマーカーを外し、直線で結ぶことが多い。分析機器を用いてしばしば得られるようなスペクトルやチャートなどはこの類になる。 2. 滑らかな曲線 まず利点を挙げよう。データ間にある真の値の振る舞いはしばしば滑らかであり、そのような場合には最も現実に即していると言える。そのため、内挿法、あるいは外挿法によってデータ点のない部分の値を推定でき、直線でつなぐより得られる情報は増える。 このような利点がある一方で、信憑性が高い印象を与えることから、誤った解釈に導いてしまう危険性があり、適用するときには細心の注意を払う必要がある。特に、データ間が開いている場合にはそこにピークなどの特徴的な挙動があるかもしれず、滑らかにつないだことによってその存在の可能性を気付けなくしてしまう恐れがある。したがって、滑らかにつなぐときには、まず挙動を十分に検討し、滑らかな振る舞いをする相応の根拠を基で行わなければならない。 3. 関数のフィッティング 最も意味のある、科学的にも発展が望める方法である。まずはフィッティングを目指し、その背後にあるメカニズムを明らかにすべく、努力すべきである。その一方で、誤った解釈に人為的に導く可能性も最も強いことから、責任を持って吟味しなければならないし、断言できるレベルの証拠が無い限りは仮説であることを明言して行わなければならない。実際には、断言できることはほとんどなく、“あるモデルに基づいて解析したところ、矛盾のない結果が得られた”と述べられれば十分である。 下の2つの図恣意的なフィッティングの例である。どちらも同じデータを用いた図であるが、左図の場合には注意しないと\(x\) と\(y\) の間に一次の関係があると信じてしまうかもしれない。特に査読を受けて掲載された、権威ある雑誌中の論文にこのような図があると、つい納得仕舞いかねない。実際にこのような例もあるので、責任を持って作成し、他人の作成したものに対しては批判的な目で評価することが求められる。 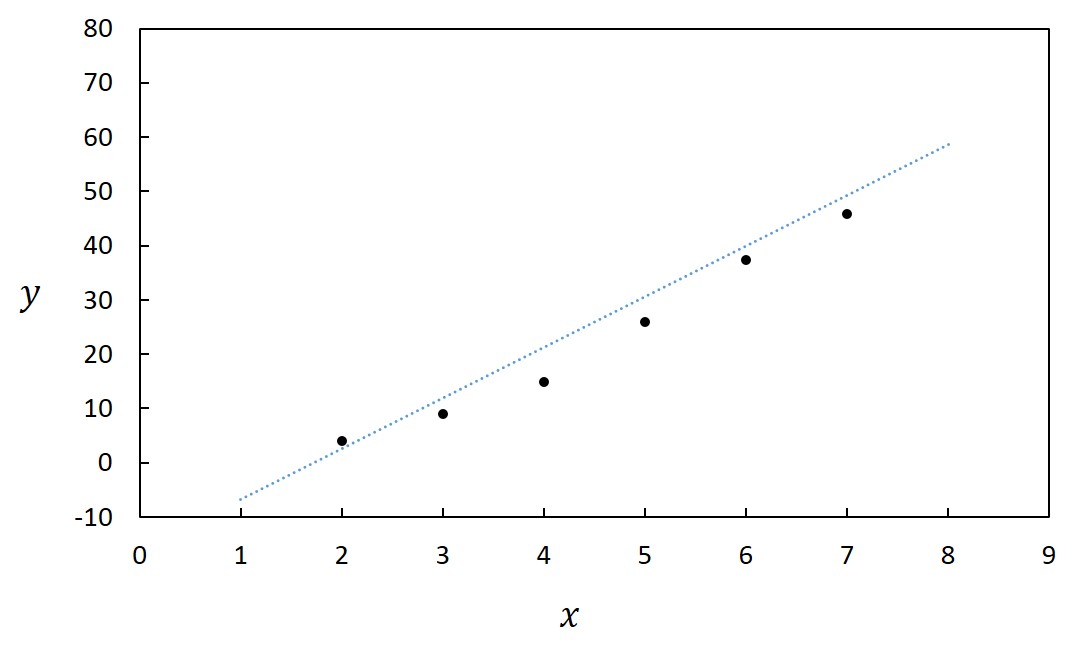 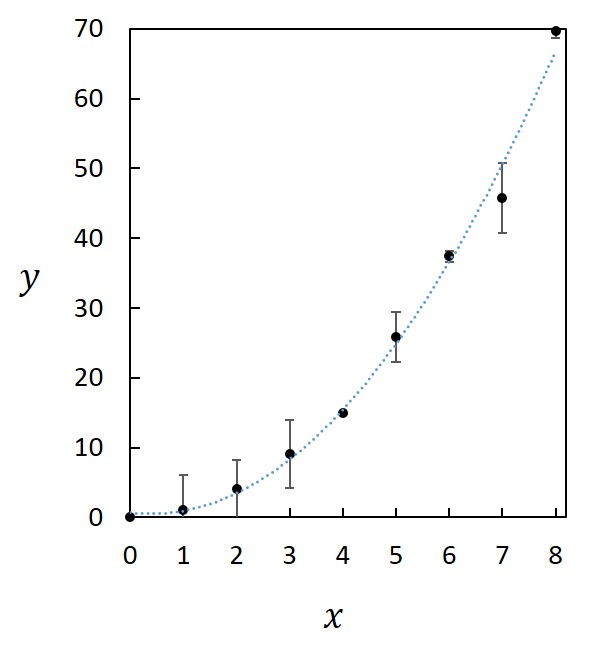 4. つながない 無根拠、無意味に直線や曲線でデータ点をつなぐより、むしろ線でつながない方が人為的な操作が加わらないだけよいと判断できる場合もある。ただし、グラフの傾向を読み取りにくくなったり、複数種のデータを示すと判別が困難になったりすることから、まずは根拠を吟味して線でつなぐ努力を払うべきである。 モデルの検証と軸の取り方 上述したように、データ点の間を線でつなぐときには、そのメカニズムを推測してモデルを立て、それに則ってフィッティングすることが望ましい。上で見た例では、\(x\) と\(y\) の間にほぼ2次の関係があることから、フィッティングを行い、2次曲線を描き入れている。しかしながら、この場合には\(y\) の代わりに\(\sqrt{y}\) を縦軸に取った下図の方がよりモデルの信憑性を吟味し易い。 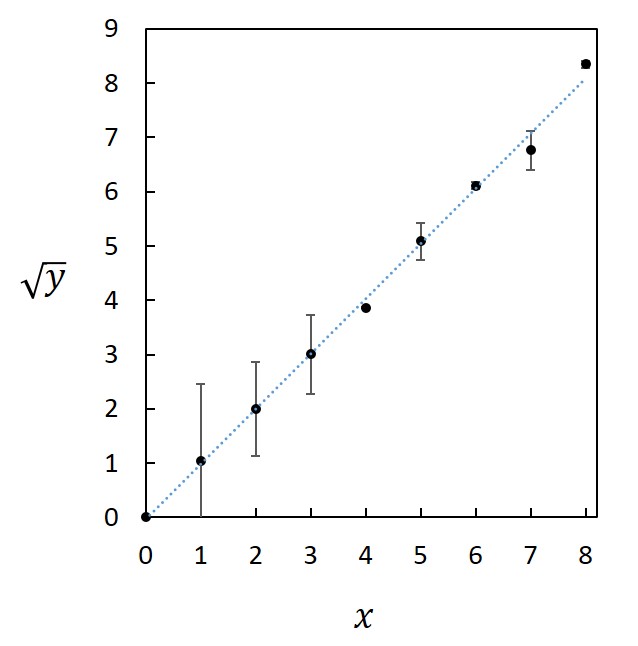 この目的で対数グラフもよく使われる。例えば粒子径を議論する場合には、1nmと2nmの粒子径の差は大きいが、1cmの粒子の径が1nm大きくなってもその差は無視できる。横軸に粒子径を取って対数表示すると、\(1-10 nm\) と\(10-100 nm\)、\(100-1000 nm\) の間隔が等しくなって相似の関係で比較できる。 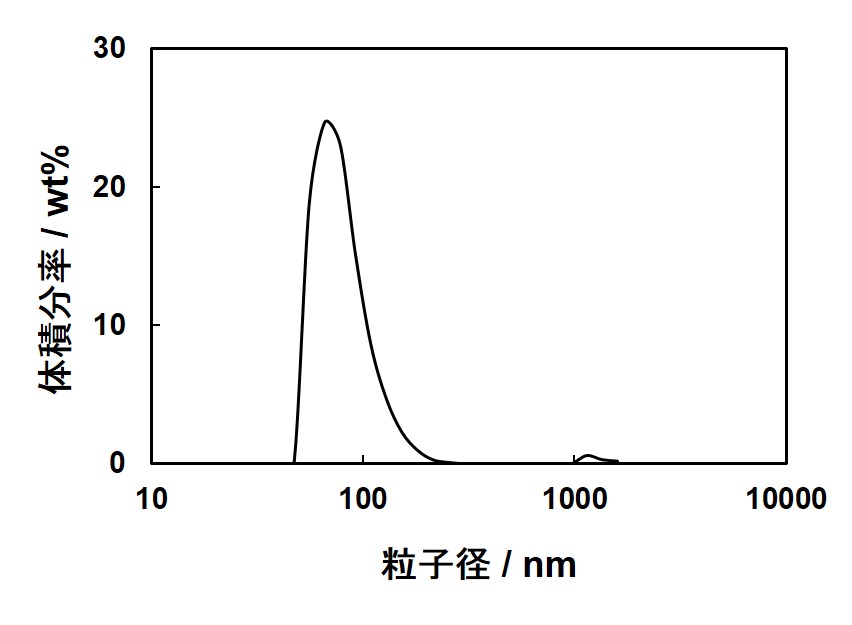 化学ではアレニウスの式のような例もある。反応速度定数\(k\)、活性化エネルギー\(E_a\)、気体定数\(R\)、絶対温度\(T\) の間に、\(A\) を定数(頻度因子)としたときに\[k=A\exp(-\frac{E_a}{RT})\]の関係が成り立つことが示されており、両辺の対数を取ると、\[\ln{k}=\ln{A}-\frac{E_a}{RT}\]が成り立つ。したがって、\(1/T\) に対する\(\ln{k}\) の関係をグラフに描く(アレニウスプロット)と、傾きから活性化エネルギー\(E_a\) が求まる。このとき用いるのが縦軸のみ対数の片対数グラフである。 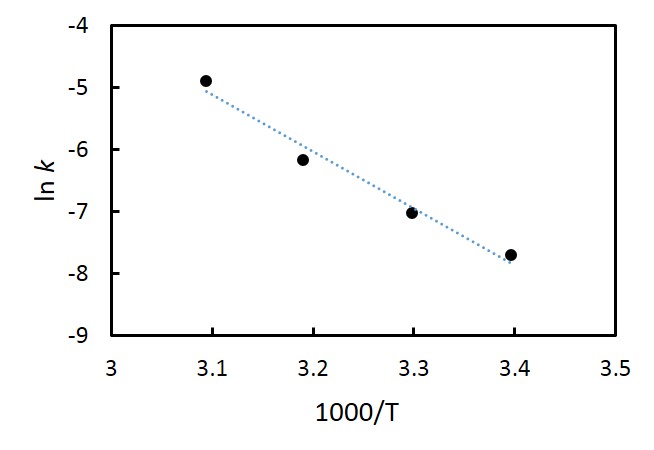 近似曲線の描き方 近似曲線は最小自乗法(最小二乗法)を使って求める。通常、グラフ作成ソフトには近似曲線作成ツールがあるので、多項式の次数、指数、対数などの関数を設定すると自動的に近似曲線が得られる。とは言うものの、最小自乗法については概要を知っておいてもらいたい。 また、評価した誤差を考慮して近似することで、より確からしい近似曲線が得られる。つまり、誤差やばらつきの小さなデータと大きなデータを同様に扱うのではなく、重み付けを行って近似曲線を求めるべきである。詳細については本講義の範疇に収まらないので、参考文献[1]のp.88以降を参照してもらいたい。 最小自乗法 \((x,y)=(x_1,y_1),\hspace{1mm}(x_2,y_2),\hspace{1mm}\cdots,\hspace{1mm}(x_i,y_i),\hspace{1mm}\cdots,\hspace{1mm}(x_n,y_n)\)のデータを\(y=f(x)\)で近似した場合、\[(x,y)=(x_1,f(x_1)),\hspace{1mm}(x_2,f(x_2)),\hspace{1mm}\cdots,\hspace{1mm}(x_i,f(x_i)),\hspace{1mm}\cdots,\hspace{1mm}(x_n,f(x_n))\]となることから、各点における誤差は、\[y_i-f(x_i)\]となり、分散は、\[\sum_{i=1}^{n}(y_i-f(x_i))^2\]となる。この分散を最小にするように係数を求めるのが最小自乗法である。 例えば、5点のデータ\((x,y)=(0,\hspace{1mm}0),\hspace{1mm}(1,\hspace{1mm}1.2),\hspace{1mm}(2,\hspace{1mm}1.7),\hspace{1mm}(3,\hspace{1mm}2.6),\hspace{1mm}(4,\hspace{1mm}4.1)\)があり、\(f(x)=ax+b\hspace{3mm}(a,b\hspace{1mm}は定数)\hspace{1mm}\)として2次式で近似式を求めたいとすると、\[(0-b)^2+(1.2-a-b)^2+(1.7-2a-b)^2+(2.6-3a-b)^2+(4.1-4a-b)^2\]\[=30a^2+5b^2-57.6a-19.2b+20ab+25.3\] |
表作成における注意事項を列挙する。
|
|
1. 化学同人編集部編, 実験データを正しく扱うために, 化学同人, 2007. 2. D.C.ベイアード, 実験法入門 実験と理論の橋渡し, ピアソン・エデュケーション, 2004. |
 Top
Top
 3 成果のまとめ方
3 成果のまとめ方