Jupyter Notebook で多成分平衡を計算する2023/09/04(月)
「Jupyter Notebook で Python を使う」の続きです。カーブフィッティングをやる予定でしたが、たまたま多成分平衡系を扱う機会があったので、そっちを先にやることにしました。
多成分の平衡が存在する時、平衡式と物質収支・電荷収支の式を立てて、連立方程式を解くことで、各成分の値を求めることができます。例えば、リン酸水溶液の三段階電離だと、電離の平衡式は下のようになります。
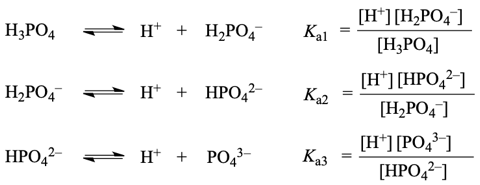
これに加えて、水の電離平衡・物質収支・電荷収支の式を立てます。([H3PO4]0は「リン酸由来の化学種の全濃度」)
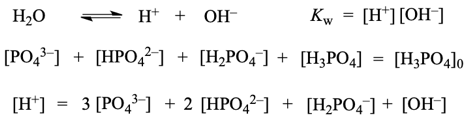
未知量が6つあって、独立な関係式が6つあるので、この連立方程式は解けます。高次方程式になるため複数個の解がありますが、物理的に意味のある解は一意に決まります。理論上はこれでおしまいです。でも、実際に計算すると、なかなか厄介です。関係式を単純に Python コードに書き起こして、非線形連立方程式を数値的に解こうとすると、うまく収束しないことがけっこうあるのです(リン酸の電離だとそうでもなさそうですが、他の平衡式を解いているときに苦労しました)。
いろいろ調べてみると、こんな論文が見つかりました。「多成分水溶液内での平衡組成の数値計算法」(三朝元勝、尾上 薫、化学工学論文集, 1993, 19, 1089. DOI:10.1252/kakoronbunshu.19.1089)。なるほど、この計算法だけで論文にする価値があるぐらいの問題だったわけですね。この論文のポイントは4つあります。(1) 1つの物質収支式に現れる化学種から1つずつ「独立成分」を選び、他の成分を平衡式を使って記述することで、独立変数の数を減らすこと。(2) 水の電離平衡が関わる時は、H+も「独立成分」とすること。(3) 物質収支式と電荷収支式(水の電離平衡が関わる場合のみ)を「〜=0」の形で記述し、これを対象関数として Newton-Raphson 法を適用すること。(4) Newton-Raphson 法の繰り返し計算において、各独立成分の濃度 C に対する増分が、濃度に対する相対値を使って Cn+1 = Cn(1 + h) という形で表されること。著者は(たぶん当然のこととして)特に言及されていませんが、(4) が地味に効果的です。平衡式では化学種ごとに濃度の値のケタが極端に異なることが多く、単純な行列計算をすると途中で破綻することがよくあるのです。
さて、Python でコーディングしてみました。まず、対象関数とその偏微分です。記号の意味は、この後のコードのコメントに書きます。
import numpy as np
import matplotlib.pyplot as plt
import math
# 多成分平衡系の組成計算
# 参考:三朝元勝、尾上 薫、化学工学論文集 1993, 19, 1089.
# https://doi.org/10.1252/kakoronbunshu.19.1089
# 対象関数とその偏微分係数行列
def target_func(Cj, Vij, Ni, Nj, Ki, Ei, Ej, E0, Qj, Ci, has_proton):
f = np.zeros(Nj)
A = np.zeros((Nj, Nj))
for i in range(Ni):
Ci[i] = Ki[i] * np.prod([np.power(Cj[j], Vij[i, j]) for j in range(Nj)])
if has_proton:
sj = 1
f[0] = E0 - sum([Ei[i] * Ci[i] for i in range(Ni)]) - sum([Ej[j] * Cj[j] for j in range(Nj)])
for k in range(Nj):
A[0, k] = Ej[0] * Cj[0] + sum([Ei[i] * Vij[i, k] * Ci[i] for i in range(Ni)])
else:
sj = 0
for j in range(sj, Nj):
f[j] = Qj[j] - (Cj[j] + sum([Vij[i,j] * Ci[i] for i in range(Ni)]))
for j in range(sj, Nj):
for k in range(Nj):
if j == k:
A[j, k] = Cj[k]
A[j, k] += sum([Vij[i,j] * Vij[i,k] * Ci[i] for i in range(Ni)])
return f, A
次に、Newton-Raphson 法の実装です。シンプルな実装なので、自前でコードを書いても大した量にはなりません。
# Xj: 独立変数とする化学種、Xi: 従属変数とする化学種
# Vij: 化学量論係数
# Xi = sum_j(V[i,j]*Xj) と記述する。例:AcO- = -(H+) + AcOH なら [-1, 1]
# Ki: 平衡定数
# Xi = Ki*(product_j(Xj^V[i,j])) と記述する。例: AcO- = Ka*[AcOH]/[H+]
# Qj: 独立変数とする化学種の物質収支
# Xj を含む平衡がすべて Xj 側に完全に偏った場合の Xj の量
# Cj: 独立変数とする化学種の初期濃度
# 省略した場合は Qj と同じとして計算を開始する
# has_proton: 平衡が H+/OH- を含むなら True
# True の場合は、最初の独立変数は H+, 最初の従属変数は OH- であるとして、電荷収支を考慮する
# Ei: 従属変数とする化学種の電荷
# Ej: 独立変数とする化学種の電荷
# E0: 系の全電荷。省略した場合は 0 とする
# max_iter: 繰り返しの最大回数
# verbose: 途中でメッセージを出すレベル
def equil_solver(Vij, Ki, Qj, Cj=None, has_proton=False, Ei=None, Ej=None, E0=0.0, max_iter=100, verbose=0):
Ni = len(Vij) # 従属変数の数
Nj = len(Vij[0]) # 独立変数の数
if Cj is None:
Cj = Qj.copy()
# 従属変数の現在値
Ci = np.zeros(Ni)
# Newton-Raphson法
converged = False
for n in range(max_iter):
f, A = target_func(Cj, Vij, Ni, Nj, Ki, Ei, Ej, E0, Qj, Ci, has_proton)
if verbose > 0:
print("f = ", f, "A = ", A)
h = np.linalg.solve(A, f)
if verbose > 0:
print("h = ", h)
mh = max(np.abs(h))
if mh < 1e-6:
converged = True
if verbose > 0:
print("Converged.")
print(Ci, Cj)
print([Ci[i]/np.prod([np.power(Cj[j], Vij[i,j]) for j in range(Nj)]) for i in range(Ni)])
break
elif mh > 1.0:
h = h / (mh * 2) # 現在値の 0.5 倍を超えて変化させない
if verbose > 0:
print("h (reduced) = ", h)
for j in range(Nj):
Cj[j] = Cj[j] * (1 + h[j])
if verbose > 0:
print("Cj = ", Cj)
return converged, Cj
ここまではどんな平衡反応でも使えるコード。では、リン酸の三段階電離に適用して、中和滴定曲線を書いてみましょう。
# 化学量論係数
# i: 従属変数
# j: 独立変数
Vij = np.array([
# 独立変数 [H+, H3PO4]
[-1, 0], # 従属変数 OH- = -(H+)
[-1, 1], # 従属変数 H2PO4- = -(H+) + H3PO4
[-2, 1], # 従属変数 HPO4(2-) = -2(H+) + H3PO4
[-3, 1] # 従属変数 PO4(3-) = -3(H+) + H3PO4
])
# 平衡定数
# それぞれの従属変数の化学種を「独立変数のみ」から生成する平衡定数
# 通常の反応式の平衡定数と比較する場合、従属変数の分子・分母に注意。
# (平衡定数を逆数にする必要がある場合がある)
Ki = np.array([
1e-14, # [OH-] = Kw/[H+]
7.5e-3, # [H2PO4-] = Ka1[H3PO4]/[H+]
7.5e-3*6.2e-8, # [HPO4(2-)] = Ka1*Ka2[H3PO4]/[H+]^2
7.5e-3*6.2e-8*2.14e-13 # [PO4(3-)] = Ka1*Ka2*Ka3[H3PO4]/[H+]^3
])
# 独立変数の電荷
Ej = np.array([1, 0]) # H+, H3PO4
# 従属変数の電荷
Ei = np.array([
-1, # OH-
-1, # H2PO4-
-2, # HPO4(2-)
-3 # PO4(3-)
])
# 独立変数の物質収支
# それぞれの独立変数を含む平衡がすべて「独立変数の化学種」側に完全に偏った時の濃度
# Qj[j] = Cj[j] + sum([Vij[i,j] * Ci[i] for i in range(Ni)])
# has_proton が True のときは Qj[0]は使われない。pH=7 を想定して 10^-7 としておく
Qj = np.array([1e-7, 0.1])
# 系内の全電荷
# Na+ のように完全電離すると仮定できる化学種がある場合、平衡には含めずに全電荷にのみ寄与すると考える
# 例:NaOH を 0.1 mol/L 加えたならば E0 = -0.1 とおける
# もちろん、原報にある通り、明示的に NaOH と Na+, OH- の平衡を含めればより厳密に計算できる
# E0 = -0.1
# 例:0.1 mol/L のリン酸を0〜3当量の NaOH で滴定した場合の pH 変化を図示
x = np.linspace(0, 0.3, 301)
y = np.zeros_like(x)
yc = np.zeros((301, 5))
for i in range(len(x)):
v = (0.1 + x[i]) / 0.1 # 元の体積を1とした時の溶液の体積(滴定すると体積が増える)
converged, Cj = equil_solver(Vij=Vij, Ki=Ki, Qj=Qj/v, has_proton=True, Ei=Ei, Ej=Ej, E0=-x[i]/v)
y[i] = -math.log10(Cj[0])
print(x[i], Cj, y[i])
yc[i, 0] = Cj[1]
yc[i, 1] = Ki[1] * Cj[1] / Cj[0]
yc[i, 2] = Ki[2] * Cj[1] / (Cj[0] ** 2)
yc[i, 3] = Ki[3] * Cj[1] / (Cj[0] ** 3)
yc[i, 4] = 0.1 / v # 全リン酸濃度
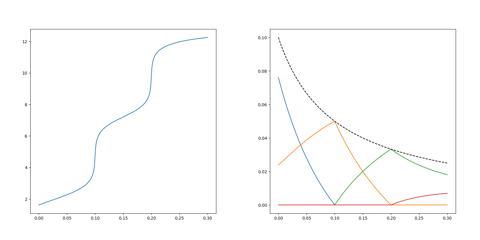
# 滴定曲線(横軸:NaOHの当量、縦軸:pH)
fig = plt.figure(figsize=(8,8))
ax = fig.add_subplot(111)
ax.plot(x, y)
# 各化学種(H3PO4, H2PO4(-), HPO4(2-), PO4(3-) の濃度(横軸:NaOHの当量)
fig2 = plt.figure(figsize=(8,8))
ax2 = fig2.add_subplot(111)
ax2.plot(x, yc[:,0])
ax2.plot(x, yc[:,1])
ax2.plot(x, yc[:,2])
ax2.plot(x, yc[:,3])
ax2.plot(x, yc[:,4], "--k")
結果はこうなりました。たぶんうまく動いています。
多段階電離の計算だけなら、わざわざ Python でコーディングしなくてもなんとかなりそうなものですが、今回わざわざ Python で書いたのは、多段階の平衡と、その他のカーブフィッティングを組み合わせて、もう少し込み入った計算をしたかったからなのです。この件はそのうち論文に盛り込む予定です。やはり汎用のプログラム言語を一つ知っておくと、いろいろ使えますね。

