特異値分解を使ったスペクトルの成分解析2024/04/04(木)
「Jupyter Notebook で多成分平衡を計算する」(2023/09/04)の続きです。え、半年も放置しちゃってたか。
こんな平衡があるとします。配位子Lが金属イオンに2個まで結合する、よくある平衡ですね。

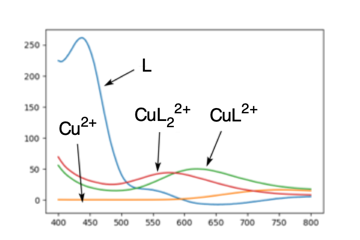
錯形成定数を求めようと思って、金属イオンの溶液に配位子を少しずつ加えて、UV-vis吸収スペクトルを測定しました。いわゆるUV-vis滴定ですね。(縦軸はモル吸光係数スケールに換算してあります)

等吸収点がないため、中間体が存在する系であることがわかります。さらに、2当量を越えると過剰の配位子の吸収が重なってきます。400 nm, 620 nm, 720 nm の吸光度の変化を当量に対してプロットしてみると、1当量と2当量のところで折れ曲がっていて、主要な平衡がここで切り替わっていることがわかります。

さて、ここから平衡定数を決めたいと思います。といっても、これはなかなか厄介です。平衡定数からモル分率を計算して、「各成分のスペクトル×モル分率」の和が実測スペクトルに合うように平衡定数を最適化すればよいのですが、問題は「各成分のスペクトル」が未知であることです。Cu2+のスペクトルは配位子=0の時のスペクトルとして確定できますが、CuL2+, CuL22+のスペクトルはどうしましょうか。配位子=1当量、2当量のときのスペクトルで近似することはできますが、本来はこの「近似」も含めて最適化したいところです。
こういう時に使えるのが、特異値分解 (singular value decomposition) です。特異値分解定理については線形代数の教科書に譲りますが、ポイントは「長方形の行列で表されるデータを、より少ない成分の重ね合わせとして近似できる」ことです。
具体的に見てみましょう。今回のデータは、滴定した各「当量」に対して、それぞれ「波長」ごとの吸光度の値があります。このデータは、「波長」×「当量」という長方形の表(行列)で表されます。この行列をAとしましょう。特異値分解定理によれば、Aは次の3つの行列の積に分解できます。ここで、UとVは直交行列、Sは対角成分以外がゼロである行列です。対角成分を大きい順に並べると、Sは一意に定まります。

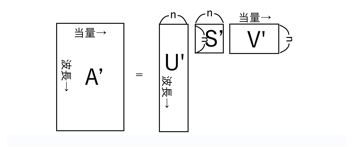
ここで、Sの対角成分を大きい方からn個とって、あとを全部ゼロで置き換えてしまいます。その行列をS'とします。下の図で、グレーの部分はすべてゼロになります。積 US'V を A' とすると、A' は A とは異なりますが、「ゼロで置き換えたSの成分」が十分に小さければ、その差は小さくできます。つまり、A' は A の近似データとして扱うことができます。

上の式は、下のように書き換えることができます。ここで、U'はUの左からn列だけをとったもの、V'はVの上からn行だけをとったものです。その他の部分はすべてゼロとの掛け算になるので、除いてしまっても結果に影響しません。
今回は、化学種が4つあるので n = 4 としました。行列 a の近似行列は、以下のコードで計算できます。
import numpy as np
numcomps = 4 # Number of components
u, s, vh = np.linalg.svd(a, full_matrices=False)
u1 = u[:,0:numcomps]
s1 = s[0:numcomps]
vh1 = vh[0:numcomps,:]
a1 = u1 @ np.diag(s1) @ vh1
最初の図と同じように、図示してみます。一目では、どこが変わったのかわからないでしょう。情報量がだいぶ減ったのですが、よく近似できていることがわかります。

面白いのは実はここからです。このデータ A' が、4つの化学種 Cu2+, CuL2+, CuL22+, L のスペクトルの重ね合わせで表されるとしましょう。平衡定数 K1, K2 としてある値を仮定して、Cu2+ の初期濃度を与えれば、加えた L の当量に対して4つの化学種のモル分率を計算できます(ここで前回の方法を使うわけです)。すると、次のような式を立てることができます。P は4つの化学種のスペクトルを横に並べたもの(この段階では未知です)、Q は4つの化学種のモル分率のリストを縦に並べたものです(K1, K2を決めれば計算できます)。

A'についての2つの式を等置すると、U'SV' = PQ となります。ここで、V'の転置行列をV'Tと置くと、Vが直交行列であることから、V'V'T = I4(I4は4x4の単位行列)となります。そこで、先ほどの式の両辺に右から V'T をかけると、U'S(V'V'T) = U'S = PQV'T となります。もし4x4行列 QV'T が正則であれば、P = U'S(QV'T)-1 となります。つまり、未知だった P が一意的に決まるのです!
実際、K1 = 2e8, K2 = 3e5 と置いて(これらの値は 400 nm の吸光度変化から手計算で推測しました)、P を計算し、4つの化学種のスペクトルを求めてみました。L のスペクトルの精度が少し悪い気がしますが、有効な測定点の数が少ないのでやむを得ません。また、このとき A' = PQ となるので、それも求めてプロットしてみました。実測データをよく再現できています。

今回は K1, K2 の値を推測して1点計算しましたが、scipy.optimize.curve_fit を使って、実測値を最もよく再現できる K1, K2 を決めることもできます。特異値分解は数学的にはかなり難解ですが、このように強力な手法なので、頑張ってマスターしておきたいですね。

