Maximaで微分方程式を解く2014/11/28（金）

反応速度を理論的に解析するときは、微分方程式を解きます。たとえば、こんな反応系の場合：

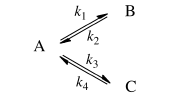
速度式はこんな風になります。

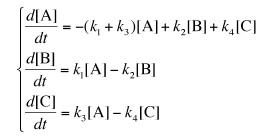
「k₁ >> k₂ かつ k₃ >> k₄」ならば生成物の比は k₁ : k₃（速度論支配）になります。一方、k₁〜k₄ が実験時間に対して十分に大きければ、生成物の比は k₁/k₂ : k₃/k₄ （熱力学支配）になります。これを導くのは簡単で、速度論支配の方は k₂ = k₄ = 0 と置けば [A] が簡単な指数関数になりますし、熱力学支配の方は平衡が達成されたと仮定して d[A]/dt = d[B]/dt = d[C]/dt = 0 と置けば単純な連立方程式になります。

速度論支配と熱力学支配の議論をするにはこれで十分なのですが、上の速度式は一見簡単な連立微分方程式なので、解析解がありそうです。ところが、これを手で解いてみようと思うと、なかなか大変です。今どき、ノートを何ページも書きつぶして微分方程式を解くなんて流行らんだろ、と思い（流行りの問題か？）、数式処理システムを使ってみました。使ったのは wxMaxima です。無料で使えます。下の画面は Mac 用のインストーラですが、Windows 用もあります。

立ち上げるといきなり真っ白な画面が出てきて戸惑いますが、ともかく次のように入力してみました。左の赤いマークは、何か入力すると現れます。入力の終わりは「shift＋リターンキー」なので注意。

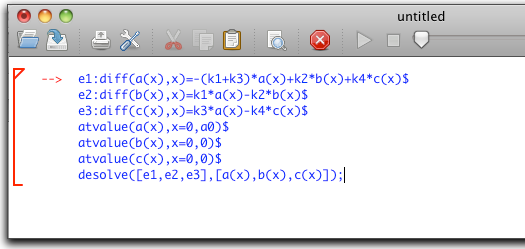
すると…

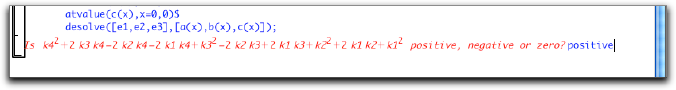
お〜なんか聞いてきたぞ。判別式か？　positive って入れたれ。

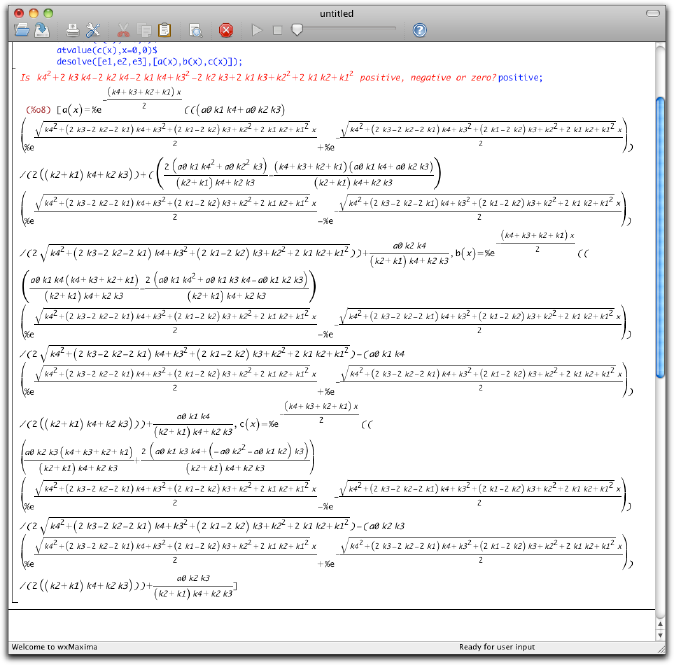
うははは、なんじゃこりゃ。手で解かんでよかった。まあとにかく、解析解があることはわかりました。（なお、上のような結果になるためには、exponentialize:true という指令を Maxima に与えておく必要があります。そうでないと、双曲線関数を使った解が表示されます。）

ここに、k₂ = k₄ = 0 を代入したらどうなるか。

ratsimp は式を簡単にするコマンドです。結果はこうなりました。

むう、もうちょい簡単にできそうですねえ。√(k3² + 2 k1 k3 + k1²) = √(k3 + k1)² = k3 + k1 とか。あと a0 をカッコでくくり出すとか。きっと何かテクニックがあるんでしょうけど、数式処理ソフトを使い慣れていないのでよくわかりません。機会があれば使い方をちゃんと勉強してみたいと思います。